目录
Arduino声级计和频谱分析仪
最近我一直在使用 Arduino 电子平台做一些项目。其中一个项目涉及对某些电机进行基准测试,并要求我测量噪音水平。我将在以后的一篇文章中更详细地介绍该项目,但现在我想写一下使用 Arduino 测量声级和分析频率的过程和最佳实践。我将讨论声音、麦克风、采样、FFT 等。本文将针那些既不是信号处理专家也不是电子专家的初学者,并且这篇文章将是相当高水平的,并为全面阅读提供了链接。
声音理论
声音是一种在空间中移动的波,当它被存储(以数字或模拟形式)时,它由波形表示,波形是在空间中某个点的每个时间点测量的波的幅度。您可以将其视为通过麦克风不断测量声音,并且测量结果形成波形。因为我们每个时间单位只能测量有限次,所以这个测量过程称为采样,它会生成离散信号。此外,由于计算机和集成电路的精度和存储空间有限,因此在此过程中每个时间样本也是离散的。
Arduino 测量信号并将它们转换成为微处理器(MCU)能够处理的逻辑的能力是由MCU上的模数转换器(ADC)提供的。因此,对于 Arduino 实现,此过程相当于将测量设备(声音麦克风)连接到 MCU,并由 ADC 以恒定速率对设备上的值进行采样。Arduino ADC 感测电压电平(通常在 0-5V 范围内)并将其转换为 0 到 1024(10 位)范围内的值。
根据我们测量的内容,声级可能非常安静或非常响亮。一方面,麦克风本身通常无法为 Arduino 提供足够的电压来感知变化。ADC 需要 5V/1024=4.8mV 的变化才能将数字值增加 1,但典型的“驻极体麦克风”可能无法为安静的声音提供如此大的电压变化。因此,麦克风通常与放大器一起使用。另一方面,非常大的噪声和高增益放大器可以将信号带到最大值5V并会有“曝光过度”或“削波”的情况,并再次使我们陷入采样无用的情况。因此,将设备和放大级别(增益)与每个用例场景相匹配非常重要。
麦克风的选择
为 Arduino 选择麦克风时,您可以获得可用的“麦克风模块”之一,该模块将麦克风与放大器或小型 PCB 上的其他逻辑结合在一起。您还可以制作自己的模块,你自己的模块可能具有能够控制麦克风和扩音器的所有不同方面的额外优势。我选择使用现成的模块,因为它比自己制作更容易、更快。
如果您的目标是录制声音并获得固定的声级,即使在不可预测的情况下,您也可以基于例如 Adafruit 的 MAX9814 来获得一款具有自动增益的模块。这样的模块会将声音“标准化”到设定的水平。对于您想要录制语音以供播放或运行频率分析的时候,这确实是正确的解决方案。不过,这不是测量音量的正确选择。为了测量音量并能够比较不同的测量结果,您需要使用可预测增益的模块。这意味着增益是不固定的,增益可以由您配置并且不会自动更改。
我评估了3个这样的模块。值得注意的是,特定的设计可能会以不同的名称出现在市场上,因为不同的制造商会使用自己的型号制造自己的设计版本。查看电路板布局并记下主芯片,以便您可以识别设备。
基于MAX4466的模块
我从Far East买了这个模块,但看起来它是基于 Adafuit 设计的。该模块具有可调节增益,您可以使用微型单匝电势计进行控制。有一个 Vcc 引脚、一个接地引脚和一个模拟输出引脚。模拟引脚发出波形,其中“0”为 Vcc/2,幅度取决于增益和声音音量。MAX4466芯片是一款专门针对麦克风放大器而优化的运算放大器,这使得该模块在这个项目里展现了出色的性能,也是我该项目的最终选择
基于 LM393 的“HXJ-17”/“Keyes”模块
我从当地的一家电子商店购买了这个模块。不知道是谁设计的,但它有一个多圈电位器,没有放大器和一个LM393比较器芯片。有一个 Vcc 引脚、一个接地引脚、一个模拟输出引脚和一个数字输出引脚。由于该模块没有放大器,因此它仅适用于感测响亮的声音,例如拍手声和敲击声。LM393 的存在允许您配置阈值,以便当声级高于阈值时,板可以生成数字输出。我能想到的与在代码中实现阈值相比的唯一优点是:1) 比较器比 MCU 的 ADC 更灵敏, 2) 或者您一开始就没有 MCU,并且将此板直接连接到继电器或类似的 IC。一些卖家宣传该模块带有 LM393 放大器,
基于LM393的“声音检测”模块
分析模拟输入
作为第一步,我建议您花一些时间分析模块的模拟输出,以查看基线和幅度。我使用以下 Arduino 函数来收集数据
#define MicSamples (1024*2)
#define MicPin A0
// measure basic properties of the input signal
// determine if analog or digital, determine range and average.
void MeasureAnalog()
{
long signalAvg = 0, signalMax = 0, signalMin = 1024, t0 = millis();
for (int i = 0; i < MicSamples; i++)
{
int k = analogRead(MicPin);
signalMin = min(signalMin, k);
signalMax = max(signalMax, k);
signalAvg += k;
}
signalAvg /= MicSamples;
// print
Serial.print("Time: " + String(millis() - t0));
Serial.print(" Min: " + String(signalMin));
Serial.print(" Max: " + String(signalMax));
Serial.print(" Avg: " + String(signalAvg));
Serial.print(" Span: " + String(signalMax - signalMin));
Serial.print(", " + String(signalMax - signalAvg));
Serial.print(", " + String(signalAvg - signalMin));
Serial.println("");
}
然后,您可以以不同的音量发出一些声音,并查看平均值、最小值、最大值和跨度值的响应情况。查看结果,您可能会发现需要调整增益电位器,以便利用声级的最大跨度,同时不要过度使用,以免削波信号。
使用 3.3V 参考电压和自由运行实现精确采样
Arduino 的 AnalogRead 功能可以轻松获取模拟引脚的数字值。它是在考虑单个样本收集的情况下实施的。在对声音进行采样时,以恒定的速率采样并准确地采样每个样本非常重要。为了实现这两个属性,我们进行以下操作。
首先,我们将配置 ADC 以使用 3.3V 作为模拟参考电压。原因是 3.3V 通常比 5V 更稳定。5V 电压可能会上下波动,尤其是当 Arduino 从 USB 连接获取电源时。3.3V 来自 Arduino 板上的线性稳压器,可以连接到 Arduino 的 ARef 引脚。这会校准我们的 ADC,将 0 至 3.3V 范围的模拟输入映射到 0 至 1024 范围的数字值。为了在电子层面实现这一点,您需要为模块提供 3.3V 电压并将 Arduino ARef 引脚连接到 3.3V。确保您的模块能够在此电压下运行。 使用以下代码来配置此模式:
analogReference(EXTERNAL); // 3.3V to AREF
其次,我们将配置 ADC 以“自由运行”模式工作,并直接从内部寄存器读取样本值,绕过analogRead。如前所述,analogRead 被设计为一次读取一个值,并且将为每次读取执行 ADC 的初始化,我们最好消除这种情况。这将使我们能够获得更可预测的采样率。
使用以下代码设置“自由运行”模式:
// register explanation: http://maxembedded.com/2011/06/the-adc-of-the-avr/ // 7 => switch to divider=128, default 9.6khz sampling ADCSRA = 0xe0+7; // "ADC Enable", "ADC Start Conversion", "ADC Auto Trigger Enable" and divider. ADMUX = 0x0; // Use adc0 (hardcoded, doesn't use MicPin). Use ARef pin for analog reference (same as analogReference(EXTERNAL)). #ifndef Use3.3 ADMUX |= 0x40; // Use Vcc for analog reference. #endif DIDR0 = 0x01; // turn off the digital input for adc0
使用以下代码读取一批示例:
for (int i = 0; i < MicSamples; i++)
{
while (!(ADCSRA & /*0x10*/_BV(ADIF))); // wait for adc to be ready (ADIF)
sbi(ADCSRA, ADIF); // restart adc
byte m = ADCL; // fetch adc data
byte j = ADCH;
int k = ((int)j << 8) | m; // form into an int
// work with k
}
第三,还可以调整ADC的速度。默认情况下,ADC 以 MCU 速度的 1:128 运行(模式 #7)。每个样本需要 ADC 大约 13 个时钟周期来处理。所以默认情况下我们得到 16Mhz/128/13=9846Hz 采样。如果我们想以双倍的速率采样,我们可以将分频器更改为 64。
以下是如何将分频器设置为 32(模式#5)的示例,它等于 16Mhz/32/13~=38Khz 的采样率:
// macros // http://yaab-arduino.blogspot.co.il/2015/02/fast-sampling-from-analog-input.html #define cbi(sfr, bit) (_SFR_BYTE(sfr) &= ~_BV(bit)) #define sbi(sfr, bit) (_SFR_BYTE(sfr) |= _BV(bit)) // 1 0 1 = mode 5 = divider 32 = 38.4Khz sbi(ADCSRA, ADPS2); cbi(ADCSRA, ADPS1); sbi(ADCSRA, ADPS0);
您可以在 github 项目的源代码中看到所有这三个代码片段一起实现。
有了这个逻辑,我们就可以获得合适的波形数据供 Arduino 处理。
声级测量
理论
声级定义为波形的幅度,可以根据代表信号一部分的样本集进行测量。
对于一个理想的正弦信号来说,振幅应该是最大的样本值。但在实际应用中,有些样本可能成为异常值,并且会对最大值产生显著影响。因此,更实际的做法是使用一个考虑所有样本值的度量标准。你可以使用平均值,但更常见的是使用均方根(RMS),它会给较高的值赋予更多的“权重”。
振幅和均方根(RMS)之间的关系是已知的,可以表示为振幅= sqrt(2)*RMS。如果我们假设声音波形与正弦波形相似,我们可以利用这个关系来基于计算得到的均方根值估计一个稳定的振幅。
我们处理的数值是相对值,而不是绝对值。毕竟,我们使用一定的增益值来调整音量水平到我们的10位数字范围内。处理声音波形时,使用相对值是非常常见的。音量通常被测量为与其他“参考点”值的比率。用于表达该比率的常用单位是分贝 (dB)。得出一个公式:
dB=10*log10(v/v0)
其中dB为电平,单位为dB,v为样本值,v0为参考值。
由于声压是一个场量,因此使用平方比,并且对数中的值“2”变为“20”[由于 log(a^b)=b*log(a)]:
dB=20*log10(v/v0)
我试图实现相对测量,我选择 v0 作为最大可能幅度(10 位 ADC 为 1024/2)。这会产生一个特定增益于我的设备的 dB 测量值,只要增益保持固定,我就可以进行多次测量并在它们之间进行有效比较。如果您想要测量绝对声级,你需要将你的水平相对于一个标准约定的声压基准值进行计算,这个基准值通常是20微帕,这是普通人感知的典型阈值。实际上,这通常是通过将特殊的校准设备连接到麦克风来完成的。该设备生成固定分贝级别的声音,您可以调整计算,使 dB 测量结果与校准设备的 dB 值相匹配。
当使用低于样本(感知阈值)的参考值时,您的 dB 值将是正值,并且随着接近最大值而变大。
有几个因素会影响实践中的测量而使这一情况变得更加复杂。首先,人耳对所有频率的敏感度并不相同。通常会对不同频段应用不同的权重。一种这样的测量单位被称为dBA,但还有其他一些略微不同的权重。其次,您的麦克风可能不会对所有频率都具有相同的灵敏度。第三,您的扬声器可能无法以相同的精确水平再现所有频率。这些复杂性需要非常精确和昂贵的设备以及特殊的校准程序,以便能够根据标准正确测量声级。要知道,这篇文章介绍的测量声级的能力非常有限,仅适合粗略的相对测量。
执行
让我们回顾一下,我们的值是 0 到 1024,代表 [-max,max],其中 1024/2=512 为“0”。我们将检索并处理样本一段时间,其中标准定义 1 秒为“慢”,125 毫秒为“快”。对于每个样本,我们将测量从“0”到样本值的距离,即该样本的幅度。然后我们可以对最大值、平均值和 RMS 进行简单的计算。我们标度上的值可以“归一化”成最大幅度的百分比或使用 dB 或两者兼而有之。这是相关的代码示例:
// consts
#define AmpMax (1024 / 2)
#define MicSamples (1024*2) // Three of these time-weightings have been internationally standardised, 'S' (1 s) originally called Slow, 'F' (125 ms) originally called Fast and 'I' (35 ms) originally called Impulse.
// modes
#define ADCFlow // read data from adc with free-run (not interupt). much better data, dc low. hardcoded for A0.
// calculate volume level of the signal and print to serial and LCD
void MeasureVolume()
{
long soundVolAvg = 0, soundVolMax = 0, soundVolRMS = 0, t0 = millis();
for (int i = 0; i < MicSamples; i++)
{
#ifdef ADCFlow
while (!(ADCSRA & /*0x10*/_BV(ADIF))); // wait for adc to be ready (ADIF)
sbi(ADCSRA, ADIF); // restart adc
byte m = ADCL; // fetch adc data
byte j = ADCH;
int k = ((int)j << 8) | m; // form into an int
#else
int k = analogRead(MicPin);
#endif
int amp = abs(k - AmpMax);
amp <<= VolumeGainFactorBits;
soundVolMax = max(soundVolMax, amp);
soundVolAvg += amp;
soundVolRMS += ((long)amp*amp);
}
soundVolAvg /= MicSamples;
soundVolRMS /= MicSamples;
float soundVolRMSflt = sqrt(soundVolRMS);
float dB = 20.0*log10(soundVolRMSflt/AmpMax);
// convert from 0 to 100
soundVolAvg = 100 * soundVolAvg / AmpMax;
soundVolMax = 100 * soundVolMax / AmpMax;
soundVolRMSflt = 100 * soundVolRMSflt / AmpMax;
soundVolRMS = 10 * soundVolRMSflt / 7; // RMS to estimate peak (RMS is 0.7 of the peak in sin)
// print
Serial.print("Time: " + String(millis() - t0));
Serial.print(" Amp: Max: " + String(soundVolMax));
Serial.print("% Avg: " + String(soundVolAvg));
Serial.print("% RMS: " + String(soundVolRMS));
Serial.println("% dB: " + String(dB,3));
}
因此,现在通过适当的模块和校准,您可以测量不同事件或设备的声级,并将它们相互比较。
使用 FHT 进行频率分析
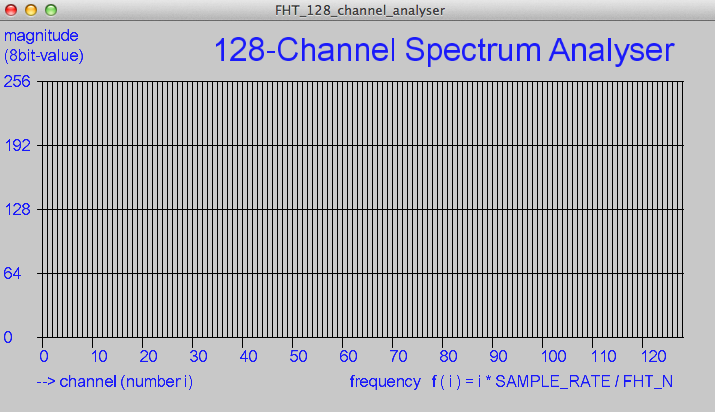
如果您想将声音“分解”为单独的频率并测量或可视化每个单独的频率,该怎么办?这可以用Arduino来完成吗?答案是肯定的,使用一些现有的库,这可以相对容易地完成。要将信号从时域转换到频域,通常会使用傅里叶变换。这种变换用于不同类型的信号,声音、图像、无线电传输等。每种信号类型都有其自己的属性,最适合声音信号的变换是离散哈莱特变换(DHT)。DHT 将使用形成波形的离散真实值。为了实现 DHT,我们将使用快速莱特利变换 (FHT),特别是ArduinoFHT 库
Arduino FHT 库可处理 16 至 256 个样本的向量。该大小表示为 N。在这个项目中,我将使用 N=256 来实现最大分辨率,但如果内存或处理能力不足,您可以使用较小的值
首先,该算法接受N个实数,并得到N/2个复数。然后我们可以将数据传递给另一个函数,计算复数的幅度,得到N/2个频率区间。最终,我们得到N/2个频率区间,每个区间覆盖sampling_rate/N Hz的频率范围。最后一个区间的最大值将为sampling_rate/2。这与信号处理理论,特别是混叠和奈奎斯特定律有关。在实践中,如果你想避免任何奇怪的效果,比如更高频率的“折叠”到较低频率上,你需要确保使用的采样率是期望声音信号中最高频率的两倍。否则,你的采样速度不够快。你也不应该过度采样,因为这会导致低ADC精度,并浪费在信号中不存在的FHT频率区间。我发现基于我的麦克风范围和典型人类听力范围,20KHz的值是一个不错的上限频率。因此,以38.4KHz(分频器=32)进行采样似乎是最佳选择。 因此对于N=256和采样率为38.4KHz,我们得到128个150Hz的频率区间,其中第一个区间保存了0-150Hz的幅度值,最后一个区间保存了19050-19200Hz的幅度值。现在我们可以专注于我们感兴趣的特定频率区间,通过串行连接发送所有频率区间的值,存储这些值,以某种方式显示它们等等。 使用数据的有趣方法之一是使用分析器进行可视化,尤其是在故障排除和开发时。将以下 FHT 示例代码加载到 Arduino 或根据您的需要进行调整。它获取样本,对数据运行 FHT,并通过串行以二进制形式发送。您的 Arduino 应连接到运行 Processing 开发环境的计算机。在处理中,加载“FHT 128 通道分析器”项目。我必须对项目进行更改以使其与Processing 3.0 兼容。为此,将对“size”函数的调用从“setup”函数中移至名为“settings”的新函数。
分析数据的另一种方法是 Arduino 以文本形式通过串行发送数据,让它运行一段时间,然后从串行监视器复制数据并将其粘贴到电子表格中。例如,使用类似于以下的代码:
void MeasureFHT()
{
long t0 = micros();
for (int i = 0; i < FHT_N; i++) { // save 256 samples
while (!(ADCSRA & /*0x10*/_BV(ADIF))); // wait for adc to be ready (ADIF)
sbi(ADCSRA, ADIF); // restart adc
byte m = ADCL; // fetch adc data
byte j = ADCH;
int k = ((int)j << 8) | m; // form into an int
k -= 0x0200; // form into a signed int
k <<= 6; // form into a 16b signed int
fht_input[i] = k; // put real data into bins
}
long dt = micros() - t0;
fht_window(); // window the data for better frequency response
fht_reorder(); // reorder the data before doing the fht
fht_run(); // process the data in the fht
fht_mag_log();
// print as text
for (int i = 0; i < FHT_N / 2; i++)
{
Serial.print(FreqOutData[i]);
Serial.print(',');
}
long sample_rate = FHT_N * 1000000l / dt;
Serial.print(dt);
Serial.print(',');
Serial.println(sample_rate);
}
然后,您可以将电子表格(例如 Excel)中的数据格式化为“3-D 曲面”网格图。例如,查看 Arduino 和 FHT 捕获并分析从 1hz 到 5000hz 的频率扫描图:
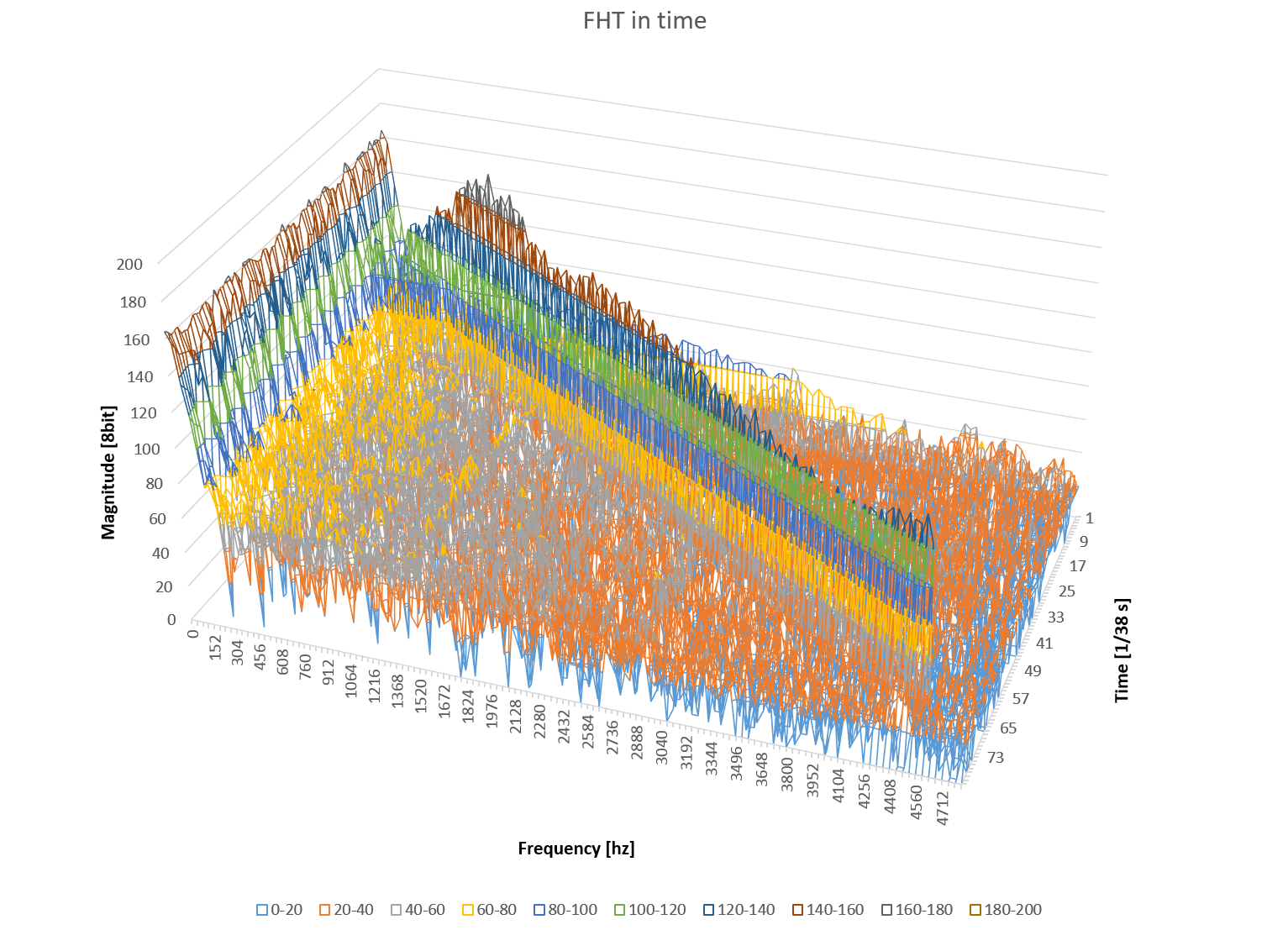
概括
我的这个项目的代码可以在 github 上找到,供你尝试。
Arduino 可用于相对声级测量和频率分析/可视化。只需要一个与用例匹配的麦克风、一个 Arduino、一些编码以及可选的 FHT 库。祝你玩得开心,如果你使用这样的设置做了一些不错的事情,请在评论中告诉我。
https://blog.yavilevich.com/2016/08/arduino-sound-level-meter-and-spectrum-analyzer/