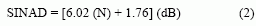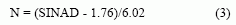ADC中的ABC:理解ADC误差对系统性能的影响
摘要:许多工程师会在设计中遇到一些很微妙的问题:ADC的规格常常低于系统要求的指标。本文介绍了如何根据系统需求合理选择ADC,列举了ADC测量中可能遇到的各种误差源。
采用12位分辨率的模数转换器(ADC)未必意味着你的系统将具有12位的精度。很多时候,令工程师们吃惊和不解的是:数据采集系统所表现出的性能往往远低于期望值。如果这个问题直到样机运行时才被发现,只好慌慌张张地改用更高性能的ADC,大量的时间被花费在重新更改设计上,同时,试投产的日程在迅速临近。问题出在哪里? 最初的分析中有那些因素发生了改变? 对于ADC的性能指标有一个深入的了解,将有助于发现一些经常导致性能指标不尽人意的细节所在。对于ADC指标的理解还有助于为你的设计选择正确的ADC。
我们从建立整个系统的性能需求入手,系统中的每个元器件都有相应的误差,我们的目标是将整体误差限定在一定的范围内。ADC是信号通道的关键部件,必须谨慎选择适当的器件。在我们开始评估整体性能之前,假设ADC的转换效率、接口、供电电源、功耗、输入范围以及通道数均满足系统要求。ADC的精度与几项关键规格有关,其中包括:积分非线性(INL)、失调和增益误差、电压基准的精度、温度效应、交流特性等。最好从直流特性入手评估ADC的性能,因为ADC的交流参数测试存在多种非标准方法,基于直流特性比较容易对两个IC进行比较。直流特性通常比交流特性更能反映器件的问题。
系统要求
确定系统整体误差的常见方法有两种:均方根和(RSS)、最差工作条件下的测试。采用RSS时,对每项误差取平均,然后求和并计算开方值。RSS误差由下式计算:
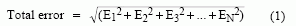
其中EN代表某个特定电路元件或参数的误差项。当所有误差不相干时这种方法最准确(实际情况可能如此,也可能不同)。利用最差条件分析法,所有误差项相加。这种方法能够确保误差植不会超出规定范围,它给出了最差条件下的误差限制,实际误差始终小于该值(通常会低出若干倍)。
多数情况下,测量误差介于两种方法测试数值之间,更接近于RSS法提供的数值。可以根据误差预算选择使用典型误差和最差工作条件下的误差。具体选择时取决于许多因素,包括:测量值的标准方差、特定参数的重要性、误差之间的相互影响程度等。由此可见,很难找到简捷的、必需遵循的规则。在我们的分析中,我们选择最差条件测试法。
在本例中,假定我们需要0.1%或者说10位的精度(1/210),这样,只有选择一个具有更高分辨率的转换器才有意义。如果是一个12位的转换器,我们可能会想当然地以为精度已足够高;但是在没有仔细检查其规格书之前,我们并没有把握得到12位的性能(实际情况可能更好或更糟)。举例来说,一个具有4LSB积分非线性误差的12位ADC,最多只能提供10位的精度(假设失调和增益误差已得到修正)。一个具有0.5LSB INL的器件则可提供0.0122%的误差或13位的精度(消除了增益及失调误差以后)。要计算最佳精度,可用最大INL误差除以2N,其中N是转换器位数。在我们的举例中,若采用0.075%误差(或11位)的ADC,则留给其余电路的误差余量只有0.025%,这其中包括传感器、前端信号调理电路(运放、多路复用器等等),或许还有数模转换器(DAC)、PWM信号或信号通路上的其它模拟电路。
我们假设整体系统的总计误差预算基于信号通道各个电路元件的误差项目总和,另外我们还假设,将要测量的是一个缓慢变化的直流、双极性输入信号,具有1kHz的带宽,工作温度范围为0°C到70°C,并在0°C至50°C范围内保证性能。
直流性能
微分非线性
虽说不被作为一项关键性的ADC参数,微分非线性(DNL)误差还是进入我们视野的第一项指标。DNL揭示了一个输出码与其相邻码之间的间隔。这个间隔通过测量输入电压的幅度变化,然后转换为以LSB为单位后得到(图1)。值得注意的是INL是DNL的积分,这就是为什么DNL没有被我们看作关键参数的原因所在。一个性能优良的ADC常常声称“无丢码”。这就是说当输入电压扫过输入范围时,所有输出码组合都会依次出现在转换器输出端。当DNL误差小于±1LSB时就能够保证没有丢码(图1a)。图1b、图1c和图1d分别显示了三种DNL误差值。DNL为-0.5LSB时(图1b),器件保证没有丢码。若该误差值等于-1LSB (图1c),器件就不能保证没有丢码,值得注意的是10码丢失。然而,当最大DNL误差值为±1时,大多数ADC都会特别声明是否有丢码。由于制造时的测试界限实际上要比规格书中所规定的更为严格,因此这种情况下通常都能够保证没有丢码。对于一个大于-1LSB (图1d中为-1.5LSB)的DNL,器件就会有丢码。
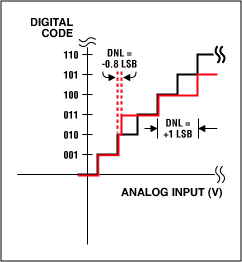
图1a. DNL误差:没有丢码。
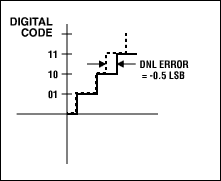
图1b. DNL误差:没有丢码。
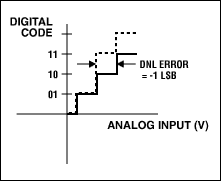
图1c. DNL误差:丢失10码。
图1d. DNL误差:AIN*数字输入是三种可能数值之一,扫描到输入电压时,10码将会丢失。
随着DNL误差值的偏移(也就是说-1LSB,+2LSB),ADC转换函数会发生变化。偏移了的DNL值理论上仍然可以没有丢码。关键是要以-1LSB作为底限。值得注意的是DNL在一个方向上进行测量,通常是沿着转换函数向上走。将造成码[N]跳变所需的输入电压值和码[N+1]时相比较。如果相差为1LSB,DNL误差就为零。如果大于1LSB,则DNL误差为正值;如果小于1LSB,DNL误差则为负值。
有丢码并非一定是坏事。如果你只需要13位分辨率,同时你有两种选择,一个是DNL指标≤ ±4LSB的16位ADC (相当于无丢码的14位),价格为5美元,另一个是DNL ≤ ±1LSB的16位ADC,价格为15美元,这时候,购买一个低等级的ADC将大幅度地节省你的元件成本,同时又满足了你的系统要求。
积分非线性
积分非线性(INL)定义为DNL误差的积分,因此较好的INL指标意味着较好的DNL。INL误差告诉设计者转换器测量结果距离理想转换函数值有多远。继续我们的举例,对于一个12位系统来讲,±2LSB的INL误差相当于2/4096或0.05%的最大非线性误差(这已占去ADC误差预算的2/3)。因此,有必要选用一个1LSB (或更好)的器件。对于±1LSB的INL误差,等效精度为0.0244%,占ADC误差预算的32.5%。对于0.5LSB的指标,精度为0.012%,仅占ADC误差预算的16% (0.0125%/0.075%)。需要注意的是,无论是INL或DNL带来的误差,都不太容易校准或修正。
失调和增益误差
失调和增益误差很容易利用微控制器(µC)或数字信号处理器(DSP)修正过来。就失调误差来讲,如果转换器允许双极性输入信号的话,操作将非常简单。对于双极性系统,失调误差只是平移了转换函数,但没有减少可用编码的数量(图2)。有两套方法可以使双极性误差归零。其一,你可以将转换函数的x或y轴平移,使负满度点与单极性系统的零点相对准(图3a)。利用这种方法,可以简单地消除失调误差,然后,通过围绕“新”零点旋转转换函数可以对增益误差进行调节。第二种技术采用了一种迭代法。首先给ADC输入施加一个0V电压并执行一次转换;转换结果反映了双极性零点失调误差。然后,通过围绕负满度点旋转转换曲线实现增益调节(图3b)。注意此时转换函数已绕A点转过一定角度,使零点偏离了期望的转换函数。因此还需要进一步的失调误差校正。
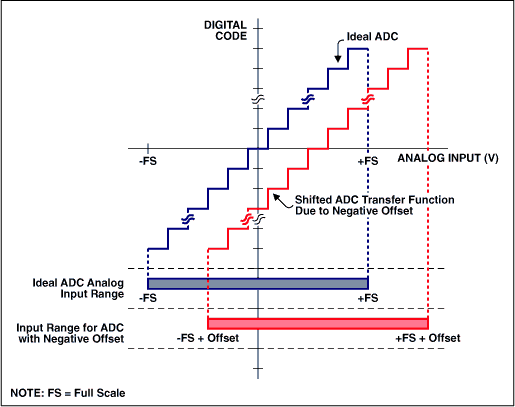 图2. 双极性系统的失调误差
图2. 双极性系统的失调误差
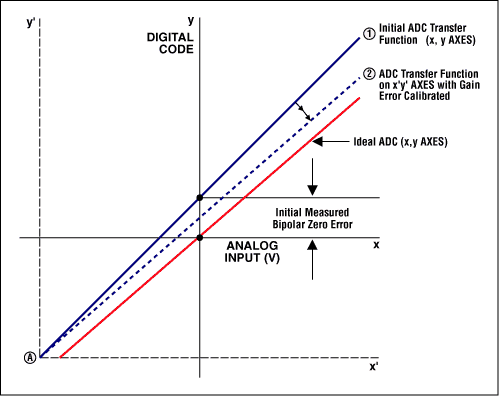
图3a.

图3b;
图3a和3b. 校正双极性失调误差(注意:阶梯状转换函数已被一条直线取代,因为该图中包含所有码,而台阶已经小得无法分辨,看上去成为一条直线)。
单极性系统还要复杂一些。如果失调为正值,可采用和双极性系统相似的处理方法。不同之处在于你将失去一部分ADC量程(见图4)。如果失调为负值,你将无法简单地通过一次转换测得失调误差。因为在零点以下,转换器只能显示出零。这样,对于一个负失调误差的转换器,你必须缓慢地增加输入电压,以确定在什么地方ADC结果出现首次跳变。同样,你将失去一部分ADC量程。
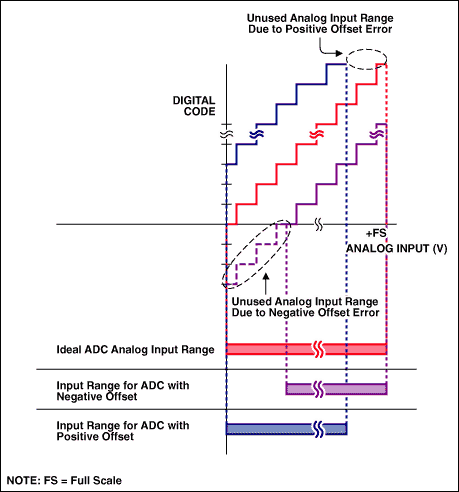
图4. 单极性系统中的失调误差
回到我们的举例,两种情况中的失调误差可按下述方法获得: 2.5V基准时+8mV的失调误差相当于12位ADC具有13LSB的误差(8mV/[2.5V/4096])。虽然分辨率仍是12位,但是你必须从每次转换结果中扣除13个码以补偿失调误差。值得注意的是,实际上这时的可测量满量程值就变为了2.5V(4083/4096) = 2.492V。此范围以上的任何值都会使ADC溢出。因此,ADC的动态范围或者说输入范围减小了。这个问题在较高分辨率的ADC中尤为显著;在16位系统中,8mV对应于210LSB (VREF = 2.5V)。 如果失调为-8mV (假设为单极性输入),接近于零的小信号输入将不会引起任何输出变化,一直到模拟输入增加到+8mV 。这同样造成了ADC动态范围的减小。 增益误差定义为满量程误差减去失调误差(图5)。满量程误差在转换函数曲线上最后一次ADC跳变处进行测量,并和理想ADC的转换函数相比较。增益误差可通过软件用一个简单的线性函数y = (m1/m2)(x)进行简单的校正,其中的m1是理想转换函数的斜率,m2是实际测得的转换函数的斜率(图5)。
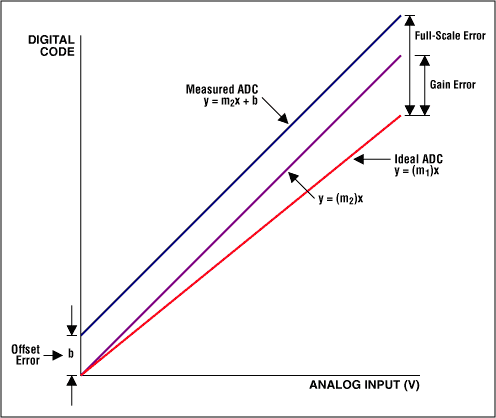
图5. 失调、增益和满量程误差
增益误差指标中可能包含或不含ADC参考电压对于误差的贡献。在电气规范中,检查一下增益误差的测试条件,并决定采用内部或外部基准工作是非常重要的。一般情况下,当采用片内基准时增益误差会比较大。如果增益误差为零,在对满量程模拟输入作转换时转换结果应为全1 (对于本例的12位系统则为3FFh) (见图6) 。由于我们的转换器不理想,全1转换结果可能会在施加的输入电压大于满量程(负增益误差)或小于满量程(正增益误差)时出现。有两种办法可以调整增益误差,其一是调节参考电压,以便在某特定参考电压下得到满量程输出,或者在软件中采用一个线性校正曲线改变ADC转换函数的斜率(一阶线性方程或查表法)。
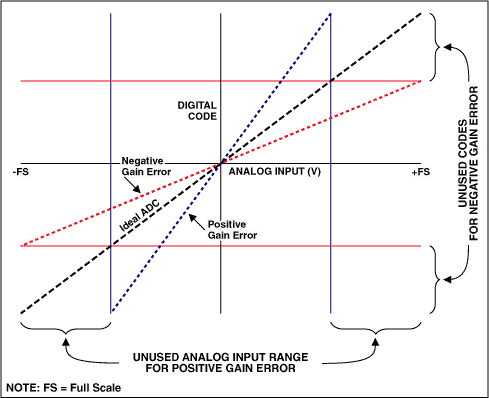
图6. 增益误差降低了动态范围
和失调误差一样,增益误差也会降低动态范围。举例来说,如果满量程输入电压时转换得到的数码输出为4050而非理想的4096 (12位转换器),也就是所谓的负增益误差,在这种情况下,高端的46个码将无法利用。类似地,如果满量程数码4096出现在输入电压低于满量程时,ADC的动态范围同样被降低了(见图6)。值得注意的是对于正的满量程误差,你无法在转换结果变为全1的点之外对转换器进行校准。
对付失调和增益误差最简单的办法就是找一个误差值足够低的ADC,这样你就不必再考虑校正了。找到一个失调和增益误差小于4LSB的12位ADC并不困难。
其它误差源
码沿噪声
码沿噪声是在转换函数中恰好发生编码跳变时出现的噪声。通常在规格书中对该项特性不作规定。甚至对于较高分辨率的转换器(16位以上),由于更小的LSB间隔,码沿噪声更为显著,通常都对这项性能未作规定。很多时候,码沿噪声能有几个LSB。转换恰好位于代码边缘的模拟输入时,代码会在LSB位发生跳动。如果出现明显的码沿噪声,就应该对采样进行平均,这样可以有效地从转换结果中去除这种噪声。需要对多少个采样取平均? 如果码沿噪声为2/3LSB RMS,这接近于4LSB P-P。那么要将噪声降低到1LSB,则需要对16次采样取平均(性能的改进正比于采样数的均方根)。
基准
采用内部或外部基准的ADC的一个最大潜在误差源是参考电压。很多情况下,内置于芯片内部的基准通常都没有足够严格的规格。为了理解基准所带来的误差源,有必要特别关注一下三项指标:温漂,电压噪声,和负载调整。
温漂
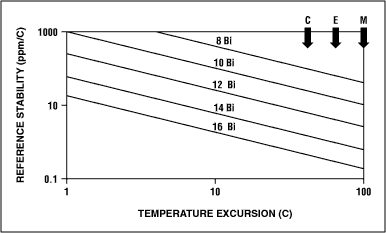
温漂是规格书中最容易被忽视的一项指标。下面的举例可以说明温度漂移是如何影响ADC性能的(图7)。对于一个12位转换器,要在整个扩展级温度范围(-40°C至+85°C)内保持精度,最大允许的温漂为4ppm/°C。不幸的是,没有任何一个ADC包含有这样高性能的片内基准。如果我们放松要求,将温度范围限制于10°C以内,那么12位ADC的参考电压最多允许25ppm/°C的温度漂移,这对于片内基准来讲仍然是相当严格的要求。即便进行多次样机测试也不能发现这种误差的严重性,因为所采用的元件通常都来自于同一批次。这样,测试结果不能反映规格书中的极端情况,这主要是由于制造工艺的变化而导致。
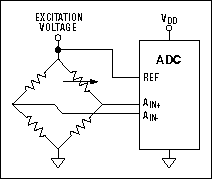
对有些系统来讲,参考电压的精度不是一个大问题,因为温度被保持于恒定,避免了温度漂移问题。还有一些系统采用一种比例测量方式,用同一个信号激励传感器和作为参考电压,可以消除基准引起的误差(图8)。因为激励源和基准同时漂移,漂移误差相互抵消。
在其它系统中,采用补偿手段消除基准漂移通常也很有效。另外也有一些系统并不关注绝对精度,而注重于相对精度。这样的系统允许基准随着时间缓慢漂移,同时又能够提供期望的精度。
电压噪声
另外一个重要指标是电压噪声。它通常规定为RMS值或峰–峰值。要估计它对于性能的影响,需要将RMS值转换为峰–峰值。如果一个2.5V基准在输出端具有500µV的峰–峰电压噪声(或83µV RMS),该噪声会带来0.02%的误差,或将系统性能限制于仅12位,而且这还没考虑任何其它的转换器误差。理想情况下,基准的噪声应该远低于一个LSB ,这样才不至于限制ADC的性能发挥。带有片内基准的ADC通常都不规定电压噪声,这样就将确定误差的任务留给了用户。如果你的设计没有达到预期性能,而你又正在使用内置基准,可尝试采用一个高性能的外部基准,这样你就可以确定造成性能下降的真正元凶是否是内部基准。
负载调整
最后一项指标是基准的负载调整。用于ADC的电压基准通常具有足够的电流可用于驱动其它器 件,因此有时也被其它IC使用。 其它元件的吸取电流会影响到电压基准,也就是说随着吸取电流的增大,参考电压会跌落。如果使用基准的器件被间歇性地打开和关闭,将会导致参考电压随之上升或下降。如果一个2.5V基准的负载调整率指标为0.55µV/µA,那就意味着当有另外一个器件吸取800µA电流时,参考电压将会改变多达440µV,这将带来0.0176%的误差(440µV/2.5V),或占去现有误差余量的几乎20%。
其它温度效应
接下来继续讨论温度相关的问题,另外还有两项指标通常很少有人关注,那就是失调漂移和增益漂移。这两项指标一般只给出典型数值,用户只能自己判断它是否足以满足系统要求。失调和增益的漂移可采用多种不同方法加以补偿。一个办法是仔细测出失调和增益漂移的完整数据,并在存储器中建立一个表格,然后随着温度的变化调节测量值。然而,这是一项繁重的任务,因为每个ADC必须单独补偿,而且补偿工序非常费时。第二个办法是只在温度发生显著变化时才执行校准。
对于那些只作一次性温度校准的系统,需要重点留意一下漂移指标。如果已校准了初始失调但温度又发生了改变,因漂移的关系又会引入新的误差,这使校准的效果被减弱。例如,假设在温度X下进行了一次转换。随后的某个时间,温度变化了10°C,又作了完全相同的另一次测量。两次读取的转换结果会有差异,这会使用户对系统的可重复性也就是可靠性产生怀疑。
有很多原因促使制造商没有给出最大界限。其中之一便是成本的增加。漂移测试需要特殊的平 台,并且还要在测试流程中增加额外的工序(这将导致额外的制造成本),以确保所有器件不超出最大漂移界限。
增益漂移的问题更多,尤其是对于那些采用内部基准的器件。这时候,基准的漂移可以一并包含于增益漂移参数中。当采用外部基准时,IC的增益漂移一般比较小,比如0.8ppm/°C。这样,±10°C的温度变化将会造成±8ppm的漂移。举例来讲,12位性能等价于244ppm (1/4096 = 0.0244% = 244ppm)。因此,±8ppm的漂移所造成的误差远低于12位系统中的一个LSB。
交流特性
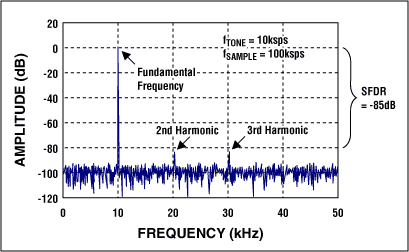
有些ADC只在输入信号接近于直流时能很好地工作。另外一些则能很好地处理从直流到Nyquist特频率的信号。仅有DNL和INL符合系统要求并不能说明转换器能够同样合格地处理交流信号。DNL和INL是在直流测试的。要掌握其交流性能就必须了解交流指标。在产品规格书中有电气参数表和典型工作特性,从中你可以找到有关交流性能的线索。需要考察的关键指标有信号–噪声比(SNR),信号–噪声加失真比(SINAD),总谐波失真(THD),以及无杂散动态范围(SFDR)。首先我们来看一看SINAD或SNR。SINAD定义为输入正弦波信号的RMS值与转换器噪声的RMS值(从直流到Nyquist特频率,包括谐波[总谐波波失真]成分)。谐波发生于输入频率的倍数位(图9)。SNR类似于SINAD,只是它不包含谐波成分。因此,SNR总是好于SINAD。SINAD和SNR一般以dB为单位。
其中N是转换器的位数。对于理想的12位转换器,SINAD为74dB。这个方程可重写为N的表达式,新的表达式揭示了能够获得的信息的位数与RMS噪声的函数关系:
这个方程就是等效位数的定义,即ENOB。
值得注意的是SINAD和输入频率有关。随着频率向Nyquist上限逼近,SINAD逐渐下降。如果规格书中的指标是在相对于Nyquist频率较低的频率下测得,在接近Nyquist频率时性能有可能变得很差。在规格书中的典型工作特性中可以找到ENOB曲线,可以观察到随着频率的增加ENOB下降,主要是由于随着输入频率的增加THD逐渐变差。例如,如果在感兴趣的频率SINAD的最小值为68dB,那么你可获得的ENOB值为11。也就是说,由于转换器的噪声和失真,你丢失了1位信息。这也意味着你的12位转换器最多只能达到0.05%的精度。记住INL是一项直流指标;ENOB是一项有关转换器对于交流信号的非线性性能指标。
SNR是不考虑失真成分的信号–噪声比。SNR反映了转换器的噪声背景。随着输入频率的增加SNR可能会急剧下降,这说明该转换器不是为该频率的应用而设计。改善SNR的一个办法是过采样,这种方法提供了一定的处理增益。过采样以远高于信号频率的速度进行采样,以此来降低转换器的噪声背景。这种方法将噪声谱扩展到更宽的频域内,这样就有效降低了一定频段内的噪声。两倍率的过采样可将噪声背景降低3dB。
SFDR定义为FFT图中,频域内输入正弦波的RMS值与最高的杂散信号的RMS值之比,一般以dB为单位。对于某些要求ADC动态范围尽可能大的通信应用,SFDR尤为重要。杂散信号妨碍了ADC对于小输入信号的转换,因为失真信号可能会比有用信号大很多。这就限制了ADC的动态范围。频域内出现一个大的杂散信号可能对SNR不会有明显影响,但会显著影响SFDR。
小结
回到我们一开始的ADC举例,假设我们将要测量直流型的信号,并且要求ADC可接受双极性输入信号,我们选择B档的MAX1241,它具有1LSB的DNL误差,1LSB的DNL误差(0.0244%),3LSB的失调误差(3/4096 = 0.0732%),以及4LSB的增益误差(0.0977%)。所有误差相加,我们得到总误差为0.1953%。我们可以校正失调和增益误差,使总误差下降到0.0244%。只要参考电压误差低于0.075% - 0.024% = 0.051%,就不会突破我们的误差预算。5ppm/°C的温漂系数在50°C的温度范围内会产生0.025%的漂移误差,这样还剩下0.026%的误差余量。要得到12位的性能,我们需要选用一个电压噪声指标低于1LSB的电压基准(这相当于2.5V/4096 = 610µV峰峰值或102µV RMS值)。温度系数5ppm/°C,宽带电压噪声30µV RMS的MAX6166是一个很好的选择。它还具有充足的供出及吸纳电流的能力,足以驱动ADC (和其它电路)。30µV噪声指标等价于180µV峰峰值,只有12位级别下一个LSB的三分之一,11位级别下(我们系统的实际要求)一个LSB的六分之一。
再检查一下MAX1241的增益漂移,资料显示该项指标为0.25ppm/°C,50°C温度范围内为12.5ppm,能够很好地满足我们的设计要求。
现在,我们就得到了一个可行的方案,再也不会出现由于对规格的考虑不周而造成的性能折扣。在本例中我们没有涉及交流性能。然而,正确理解ADC的技术指标,以及它们如何对转换器的性能产生作用,无疑将使你具备足够的知识,能够从众多产品中选择出满足你性能要求的适当的ADC。
原文地址:https://www.maximintegrated.com/cn/app-notes/index.mvp/id/748